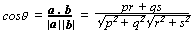Amaths5
PARAMETRIC EQUATIONS
Curve defined by; x = f(t), y g(t), t = parameter
Cartesian equation obtained when t is eliminated
if x = f(θ), y = g(θ): use
sinθ + cosθ = 1, cos2θ = cos2θ - 1 = 1 - 2sin2θ, sin2θ = 2sinθcosθ
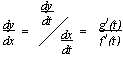
VECTORS
a = b  |a| = |b|, a & b same direction
|a| = |b|, a & b same direction
a = - b  |a| = |b|, a & b opposite direction
|a| = |b|, a & b opposite direction
a = unit vector  |a| = 1
|a| = 1
a = zero vector  |a| = 0
a + b = b + a (commutative law)
|a| = 0
a + b = b + a (commutative law)
unit vector in direction of a:
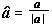
Parallel vectors
b = ka; k < 0: opposite direction, k > 0: same direction 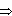 |b| = |k||a|
|b| = |k||a|
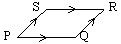
Triangle law:
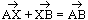

Parallelogram law:
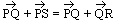
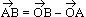
pa + qb = ra + sb  p = r, q = s (a & b = non-parallel and non-zero vectors)
p = r, q = s (a & b = non-parallel and non-zero vectors)
Position vectors
(1) relative to origin O, position vector of P is 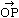 , (2)A, B and C are collinear pts
, (2)A, B and C are collinear pts 
Vectors in a Cartesian plane
P = (x, y), 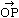 = xi + yj (i = unit vector along x-axis, j = unit vector along y-axis)
= xi + yj (i = unit vector along x-axis, j = unit vector along y-axis)
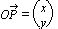
unit vector in direction of
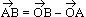
=
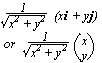
SCALAR PRODUCT
of two non-zero vectors
a . b = |a||b|cosθ (θ = angle bet a and b)
a . b = b . a (commutative law)
a . (b + c) = a . b + a . c (distributive law)
λ(a . b) = a . (λb) = (λa) . b = l |a||b|cosθ
a . b = 0  a & b are perpendicular vectors
a & b are perpendicular vectors
a . a = |a|2 = a2
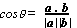
of vectors in the Cartesian plane
a = pi + qj, b = ri + sj
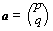
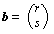
a . b = pr + qs
a is perpendicular to b  a . b = 0
a . b = 0  pr + qs = 0
pr + qs = 0
a . a = p2 + q2
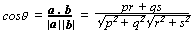
Amaths1
Amaths2
Amaths3
Amaths4
Back to 'O' level notes index
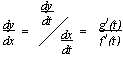
 |a| = |b|, a & b same direction
|a| = |b|, a & b same direction |a| = |b|, a & b opposite direction
|a| = |b|, a & b opposite direction |a| = 1
|a| = 1 |a| = 0
a + b = b + a (commutative law)
|a| = 0
a + b = b + a (commutative law)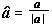
 |b| = |k||a|
|b| = |k||a|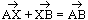

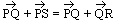

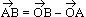
 p = r, q = s (a & b = non-parallel and non-zero vectors)
p = r, q = s (a & b = non-parallel and non-zero vectors)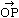 , (2)A, B and C are collinear pts
, (2)A, B and C are collinear pts 
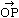 = xi + yj (i = unit vector along x-axis, j = unit vector along y-axis)
= xi + yj (i = unit vector along x-axis, j = unit vector along y-axis)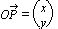
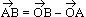
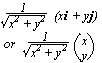
 a & b are perpendicular vectors
a & b are perpendicular vectors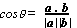
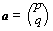
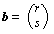
 a . b = 0
a . b = 0  pr + qs = 0
pr + qs = 0