Amaths2
TRIGONOMETRIC FUNCTIONS
sin θ°= cos (90 - θ)°
cos θ =sin (90 - θ)°
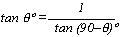
Special angles
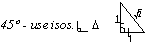
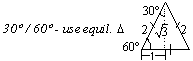
General angles
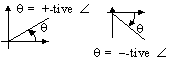
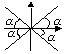
α = basic/associated acute/reference angle
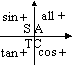
For any θ° with basic α
sin θ° = sinα [1st + 2nd]
sin θ° = -sinα [3rd + 4th]
cos θ° = cosα [1st + 4th]
cos θ° = -cosα [2nd + 3rd]
tan θ° = tanα [1st + 3rd]
tan θ° = -tanα [2nd + 4th]
cos (-θ°) = cosθ°
sin (-θ°) = - sinθ°
tan (-θ°) = - tanθ°
Sine, Cosine, Tangent Graphs
sin 0° = 0
sin 30° = 0.5
sin 90° = 1
sin 150° = 0.5
sin 180° = 0
sin 210° = -0.5
sin 270° = -1
sin 330° = -0.5
sin 360° = 0
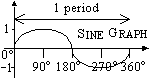
cos 0° = 1
cos 60° = 0.5
cos 90° = 0
cos 120° = -0.5
cos 180° = -1
cos 240° = -0.5
cos 270° = 0
cos 300° = 0.5
cos 360° = 1
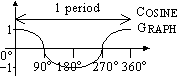
tan 0° = 0
tan 45° = 1
tan 90° = undefined
tan 135° = -1
tan 180° = 0
tan 225° = 1
tan 270° = undefined
tan 315° = -1
tan 360° = 0
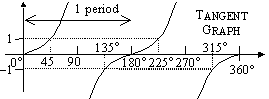
secant : secθ° = 1/cosθ°, cos θ°  0
0
cosecant : cosecθ° = 1/sinθ°, sin θ°  0
0
cotangent : cotθ° = 1/tanθ°, tan θ°  0
0
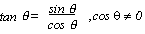
sin2θ° + cos2θ° = 1
sec2θ° = 1 + tan2θ°
cosec2θ° = 1 + cot2θ°
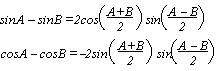
Addition & Subtraction Formulae
sin (θ ± α) = sin θcosα ± cosθsinα
cos (θ ± α) = cosθcosα 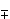 sinαsinθ
sinαsinθ
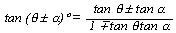
Double Angle Formula
cos2A = cos2A - sin2A = 2cos2A - 1 = 1- 2sin2A
sin2A = 2sinAcosA
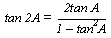
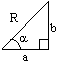
a cosθ° ± b sinθ°
a cosθ° ± b sinθ° = R cos (θ 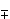 α)°
α)°
a sinθ° ± b cosθ° = R cos (θ ± α)°
Amaths3
Amaths4
Amaths5
Amaths1
Back to 'O' level notes ind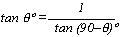
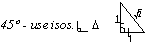
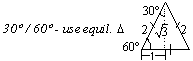
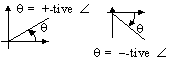

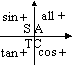
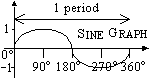
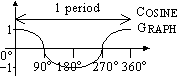
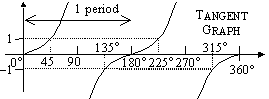
 0
0 0
0 0
0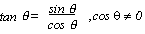
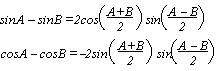
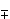 sinαsinθ
sinαsinθ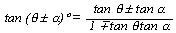
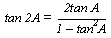
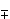 α)°
α)°