Amaths4
DIFFERENTIATION
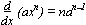
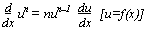
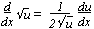
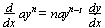
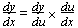
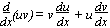
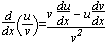
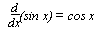
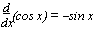
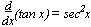
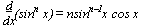
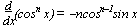
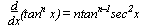
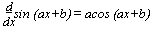
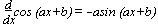
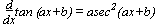
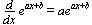

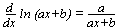
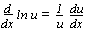
f(x) = ln x  f-1(x) = ex
f-1(x) = ex
y=ln(ax+b): can be defined for ax+b>0, intersects x-axis at x-coordinate: ax+b =1, asymtote: ax+b=0
Rate of change
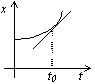
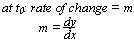
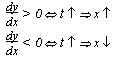
Increasing at a steady rate: x = mt + c
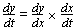
Small changes
(x1, y1) > (x2, y2), δy = y2 - y1, δx =x2 - x1
dx > 0 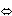 increase in x, x2 - x1 > 0
increase in x, x2 - x1 > 0
dx < 0 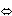 decrease in x, x2 - x1 < 0
decrease in x, x2 - x1 < 0
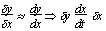
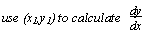
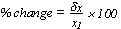
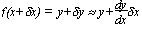
Stationery pt/ turning pt/ stationery (max/min value of y)
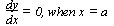
Stationery:-pt = (a, f(a)), -value of y = f(a)
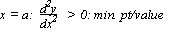
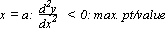
Motion of a particle
s = dist/displacement from starting/fixed pt O
P: instantaneously at rest, v = 0
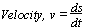
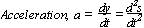
INTEGRATION
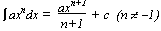
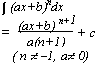
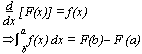
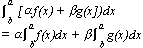
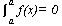
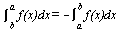
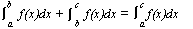
 [αf(x)+ βg(x)]dx = α
[αf(x)+ βg(x)]dx = α f(x)dx + β
f(x)dx + β g(x)dx (α, β = constants)
g(x)dx (α, β = constants)
 cos x dx = sin x + c
cos x dx = sin x + c
 sin x dx = -cos x + c
sin x dx = -cos x + c
 tan x dx = sec2 x + c
tan x dx = sec2 x + c
 cos(ax+b) dx = a-1 sin(ax+b) + c
cos(ax+b) dx = a-1 sin(ax+b) + c
 sin(ax+b) dx = -a-1 cos(ax+b) + c
sin(ax+b) dx = -a-1 cos(ax+b) + c
 tan(ax+b) dx = a-1 sec2(ax+b) + c
tan(ax+b) dx = a-1 sec2(ax+b) + c
 e(ax+b) dx = a-1e(ax+b) + c (a
e(ax+b) dx = a-1e(ax+b) + c (a 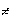 0)
0)
 (ax+b)-1 dx = a-1ln(ax+b) + c (a
(ax+b)-1 dx = a-1ln(ax+b) + c (a 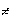 0, ax+b > 0)
0, ax+b > 0)
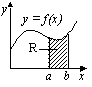
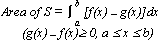
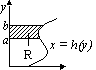
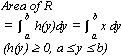
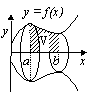
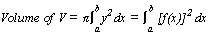
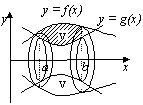
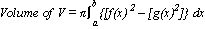
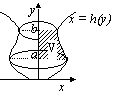
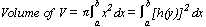
Kinematics
at time t; displacement, x =  v dt = a dtdt, velocity, v =
v dt = a dtdt, velocity, v =  a dt, (av. velocity = displacement/ time)
a dt, (av. velocity = displacement/ time)
Amaths5
Amaths1
Amaths2
Amaths3
Back to 'O' level notes index
Back to notes index
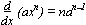
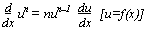
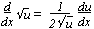
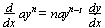
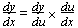
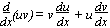
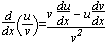
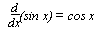
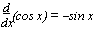
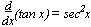
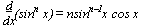
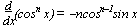
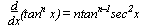
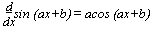
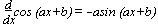
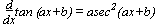
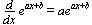

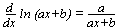
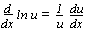
 f-1(x) = ex
f-1(x) = ex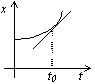
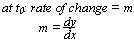
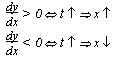
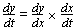
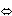 increase in x, x2 - x1 > 0
increase in x, x2 - x1 > 0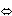 decrease in x, x2 - x1 < 0
decrease in x, x2 - x1 < 0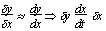
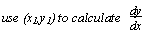
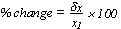
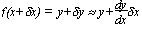
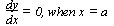
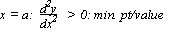
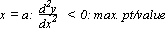
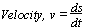
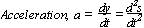
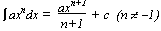
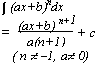
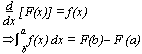
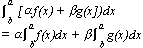
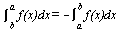
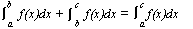
 [αf(x)+ βg(x)]dx = α
[αf(x)+ βg(x)]dx = α f(x)dx + β
f(x)dx + β g(x)dx (α, β = constants)
g(x)dx (α, β = constants) cos x dx = sin x + c
cos x dx = sin x + c sin x dx = -cos x + c
sin x dx = -cos x + c tan x dx = sec2 x + c
tan x dx = sec2 x + c cos(ax+b) dx = a-1 sin(ax+b) + c
cos(ax+b) dx = a-1 sin(ax+b) + c sin(ax+b) dx = -a-1 cos(ax+b) + c
sin(ax+b) dx = -a-1 cos(ax+b) + c tan(ax+b) dx = a-1 sec2(ax+b) + c
tan(ax+b) dx = a-1 sec2(ax+b) + c e(ax+b) dx = a-1e(ax+b) + c (a
e(ax+b) dx = a-1e(ax+b) + c (a 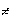 0)
0) (ax+b)-1 dx = a-1ln(ax+b) + c (a
(ax+b)-1 dx = a-1ln(ax+b) + c (a  0, ax+b > 0)
0, ax+b > 0)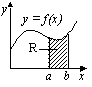
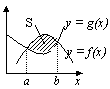
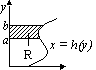
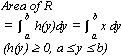
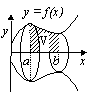
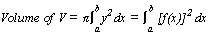
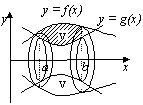
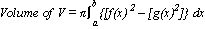
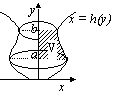
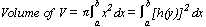
 v dt = a dtdt, velocity, v =
v dt = a dtdt, velocity, v =  a dt, (av. velocity = displacement/ time)
a dt, (av. velocity = displacement/ time)