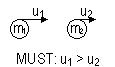DYNAMICS
Momentum
-all moving obj.s have momentum, more momentum > greater 'impact' when hits something
momentum, p = mass, m × vel,v > p = mv , p: units = Ns / kgm/s (p = linear momentum)
-same dirn as vel, unbalance forces on obj > change in vel > change in momentum
 p = pfinal - pinitial = pf - pi
p = pfinal - pinitial = pf - pi
mass: property of a body to resist change in momentum
(inertia- tendency for a body to remain at rest / if moving, to continue its motion in a straight line, ie tendency to remain in state of motion)
weight: effect of gravitational field on a mass / force of pull of gravity on a mass
Newtons 1st law of motion: every obj continues in its state of rest or uniform motion in a straight line unless it is compelled to change that state by a net external force acting upon it (internal forces don't affect motion)
no force > no change in vel > no acc
Newtons 2nd law of motion: the rate of change of momentum of a body is proportional to the total force acting on it & occurs in the dirn of the force
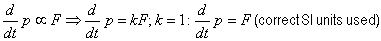
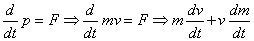

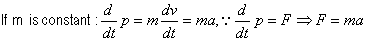
F=ma (F must be resultant force): 1N = force which gives 1kg an acc of 1m/s2
Newtons 3rd law of motion: if body A exerts a force o body B, then body B exerts an opposite force of the same size on body A (every action has an equal and opposite reaction) (2 bodies, 2 forces)
F = ma > F = m ( v/
v/ t) > F
t) > F t = m
t = m v (
v ( p = m
p = m v) >
v) >  p = F
p = F t (mass & force: const)
t (mass & force: const)
 p = F
p = F t = vector quan: impulse of a force (units = Ns) (dirn of impulse = dirn of
t = vector quan: impulse of a force (units = Ns) (dirn of impulse = dirn of  p)
p)
impulse = area under force-time graph
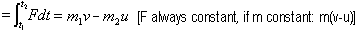
Conservation of momentum: total momentum of a system is constant provided no resultant external force acts on it
external forces: friction / gravity,.. (must be in closed system)  p of one obj: equal and opposite of
p of one obj: equal and opposite of  p of other obj
p of other obj
inelastic collision: loss of KE > heat / change in shape / sound,
(perfectly) elastic collision: no loss in KE
perfectly inelastic collision: not all KE lost, but obj.s stick together > move as 1
(all KE lost is possible if same mass + same vel in head-on collision)
glancing collision: one obj stationery
For perfectly elastic collisions, rel speed of approach = rel speed of separation
Verification of statement 'for perfectly elastic collisions, rel speed of approach = rel speed of separation'
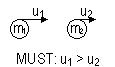
rel speed of approach = u1 - u2
rel speed of separation = v2 - v1 [MUST: p = pfinal - pinitial = pf - pi
p = pfinal - pinitial = pf - pi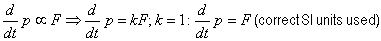
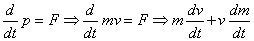

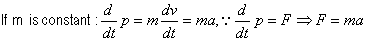
 v/
v/ t) > F
t) > F t = m
t = m v (
v ( p = m
p = m v) >
v) >  p = F
p = F t (mass & force: const)
t (mass & force: const) p = F
p = F t = vector quan: impulse of a force (units = Ns) (dirn of impulse = dirn of
t = vector quan: impulse of a force (units = Ns) (dirn of impulse = dirn of  p)
p)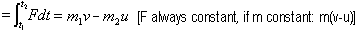
 p of one obj: equal and opposite of
p of one obj: equal and opposite of  p of other obj
p of other obj