CURRENT OF ELECTRICITY
Electric charge
charge(+/-), Q which flows past a pt. in time, t if current, I is constant is defined by Q = It (Q = coulomb, C, 1C = 1As)
if I not const, Q = 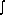 I dt (area under I-t graph) [Q = It => I = dQ/dt => Q =
I dt (area under I-t graph) [Q = It => I = dQ/dt => Q = 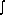 I dt]
I dt]
I = nAve [n = # of conduction electrons per unit volume, A = cross-sectional area of wire, v = drift speed/velocity of e-s, e = electric charge] (I = nAvQ; Q for both + & - charges) (v depends on ion vibration; vib. ^: v decreases (more collisions)
dirn of conventional current = dirn of +ve charges (+ > -)
current, I = rate of flow of charge
Potential difference
-pd bet 2 pts = E converted from elec E to other forms of E when unit charge passes from 1 pt to another
pd = E converted/charge => V= E/Q (1 V = 1 J/C)
-potential at a pt in circuit: usually pd bet pt & arbitrary zero (arbitrary zero: electric earth)
V = E/Q = E/t ÷ Q/t = P/I => pd = power/current (1 V = 1 W/A)
Resistance
-electric property of material that makes moving charges -dissipate energy
-ratio of pd to current, R= pd/current = V/I (R:  , ohm, 1 = 1 V/A)
, ohm, 1 = 1 V/A)
Ohm's Law: I through a metallic conductor is directly ∝ to the pd across its ends, provided temp remains const
grad of V-I graph = R
grad of I-V graph = 1/R

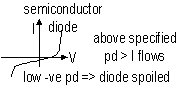
1/R = conductance (S, siemens, 1 S =  -1)
-1)
R ∝ l/A => R = k l/A =  l/A (
l/A ( = resistivity = RA/ l;
= resistivity = RA/ l;  m)
m)
 (
( m); conductor: ~107, semiconductor: ~102, insulator: ~1010
m); conductor: ~107, semiconductor: ~102, insulator: ~1010
Rt = R0(1 +  t) [
t) [ = temp coefficient of resistance]
= temp coefficient of resistance]
 = (Rt - R0) / R0t
= (Rt - R0) / R0t
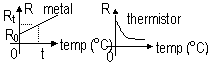
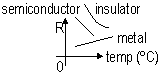
I = nAve: as T 
-metals; n: ~ const (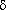
 ), v:
), v: 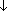 => I:
=> I: 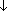 => R:
=> R: 
-thermistor; n:  , v:
, v:  => I:
=> I:  => R:
=> R: 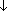 -insulator; n:
-insulator; n:  => I:
=> I:  => R:
=> R: 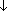
-semiconductor; n:  , v:
, v: 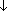 => I:
=> I:  (
( in charge carriers more significant)=> R:
in charge carriers more significant)=> R: 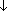
conductivity = 1/ resistivity = 1/
I = V/R = VA/( l) = conductivity x VA/ l
l) = conductivity x VA/ l  I ∝ conductivity, pd, cross-sectional area & I ∝ 1/wire length
I ∝ conductivity, pd, cross-sectional area & I ∝ 1/wire length
Electromotive force
-E converted from other forms to elec E per unit charge
emf, 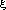 = energy converted (generated) / charge supplied,
= energy converted (generated) / charge supplied, 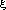 = E/Q (
= E/Q (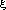 : volts, V, 1 V = 1 J/C)
: volts, V, 1 V = 1 J/C)
emf of source = pd across source terminal as I  0
0
Internal Resistance
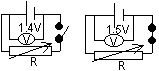
When I flows through resistor: voltmeter shows pd across battery & resistor (voltage drop due to voltage drop in int R)
E transferred per second within battery = E (transferred in circuit & in overcoming int R) per second
I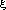 = I2R + I2r
= I2R + I2r
=> 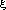 = IR +Ir
= IR +Ir
=> V = IR = 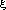 - Ir = emf - voltage across int R = terminal pd (pd shown on voltmeter)
- Ir = emf - voltage across int R = terminal pd (pd shown on voltmeter)
good voltmeter: v. high R- accurate reading: terminal pd very close to battery emf
V = IR = 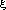 -Ir (r: const)
-Ir (r: const)
 if R (resistance of resistor) is varied and I measured => V-I graph plotted to obtain r
if R (resistance of resistor) is varied and I measured => V-I graph plotted to obtain r
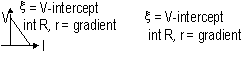
Efficiency
efficiency = power (output / input) = power [to external circuit / used(supplied)] = I2R/I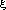 = IR/
= IR/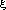 = IR/(IR+Ir) = R/(R+r)
= IR/(IR+Ir) = R/(R+r)
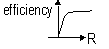
efficiency  1 unless r = 0
1 unless r = 0
R >> r, efficiency  1
1
R = r, efficiency = 50% (max power)
Back to 'A' level notes index
Back to notes index
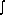 I dt (area under I-t graph) [Q = It => I = dQ/dt => Q =
I dt (area under I-t graph) [Q = It => I = dQ/dt => Q = 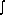 I dt]
I dt] , ohm, 1 = 1 V/A)
, ohm, 1 = 1 V/A)
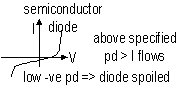
 -1)
-1) l/A (
l/A ( = resistivity = RA/ l;
= resistivity = RA/ l;  m)
m) (
( m); conductor: ~107, semiconductor: ~102, insulator: ~1010
m); conductor: ~107, semiconductor: ~102, insulator: ~1010 t) [
t) [ = temp coefficient of resistance]
= temp coefficient of resistance] = (Rt - R0) / R0t
= (Rt - R0) / R0t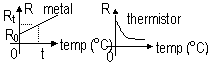


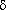
 ), v:
), v: 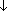 => I:
=> I: 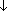 => R:
=> R: 
 , v:
, v:  => I:
=> I:  => R:
=> R: 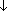 -insulator; n:
-insulator; n:  => I:
=> I:  => R:
=> R: 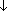
 , v:
, v: 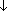 => I:
=> I:  (
( in charge carriers more significant)=> R:
in charge carriers more significant)=> R: 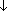

 l) = conductivity x VA/ l
l) = conductivity x VA/ l  I ∝ conductivity, pd, cross-sectional area & I ∝ 1/wire length
I ∝ conductivity, pd, cross-sectional area & I ∝ 1/wire length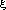 = energy converted (generated) / charge supplied,
= energy converted (generated) / charge supplied, 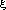 = E/Q (
= E/Q (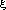 : volts, V, 1 V = 1 J/C)
: volts, V, 1 V = 1 J/C) 0
0
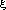 = I2R + I2r
= I2R + I2r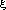 = IR +Ir
= IR +Ir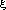 - Ir = emf - voltage across int R = terminal pd (pd shown on voltmeter)
- Ir = emf - voltage across int R = terminal pd (pd shown on voltmeter)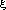 -Ir (r: const)
-Ir (r: const) if R (resistance of resistor) is varied and I measured => V-I graph plotted to obtain r
if R (resistance of resistor) is varied and I measured => V-I graph plotted to obtain r 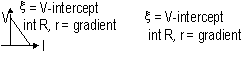
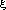 = IR/
= IR/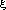 = IR/(IR+Ir) = R/(R+r)
= IR/(IR+Ir) = R/(R+r)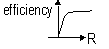
 1 unless r = 0
1 unless r = 0 1
1