 /4 => f0 = v/
/4 => f0 = v/ = v/4l
= v/4l /2 => f0 = v/
/2 => f0 = v/ = v/2l
= v/2l 1/4 => f1 = v/
1/4 => f1 = v/ 1 = 3v/4l = 3f0
1 = 3v/4l = 3f0 1 => f1 = v/
1 => f1 = v/ 1 = v/l = 2f0
1 = v/l = 2f0 2/4 => f2 = v/
2/4 => f2 = v/ 2 = 5v/4l = 5f0
2 = 5v/4l = 5f0 2/2 => f2 = v/
2/2 => f2 = v/ 2 = 3v/2l = 3f0
2 = 3v/2l = 3f0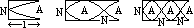

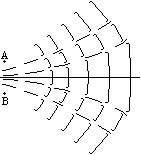
 /2 nearer to A)
/2 nearer to A) (k
(k  Z+)
Z+) (k
(k  Z+)
Z+)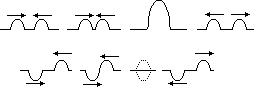
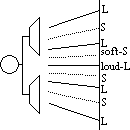
 ), in phase/ w/ const phase diff
), in phase/ w/ const phase diff of light is v.small (not close: light & dark bands v.close => can't be seen)
of light is v.small (not close: light & dark bands v.close => can't be seen)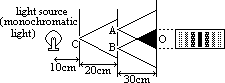



 PMO
PMO 
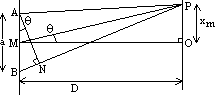
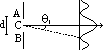
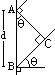
 BAN =
BAN = 
 BAN: sin
BAN: sin = BN/AB = m
= BN/AB = m /a
/a PMO: tan
PMO: tan = PO/MO = xm/D
= PO/MO = xm/D is v.small, tan
is v.small, tan
 sin
sin => xm/D = m
=> xm/D = m /a => xm = mD
/a => xm = mD /a
/a /a
/a fringe separation, x = D
fringe separation, x = D /a [D: separation of double slit & screen, a: separation of double slit,
/a [D: separation of double slit & screen, a: separation of double slit,  : wavelength of wave]
: wavelength of wave] light: 10-6m
light: 10-6m ) closest to central, red fringe (largest
) closest to central, red fringe (largest  ) furthest from central
) furthest from central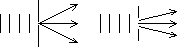
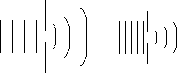
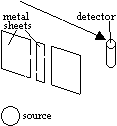
 ) > more diffraction
) > more diffraction light= 6 × 10-7m => small objects/ aperture: sig diffraction of light
light= 6 × 10-7m => small objects/ aperture: sig diffraction of light (low notes heard easier than high notes)
(low notes heard easier than high notes)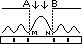
 )
) =
=  /d (d: separation of double slit)
/d (d: separation of double slit) 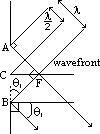
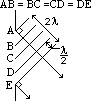

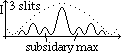
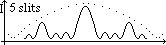
 = path diff bet 2 adjacent slits
= path diff bet 2 adjacent slits (k = whole #/0)
(k = whole #/0) = BC/AB = k /d => dsin
= BC/AB = k /d => dsin = k
= k
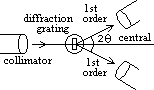
 =>
=>  = dsin
= dsin (k = 1)
(k = 1)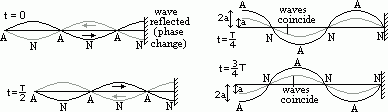
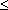 A
A 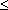 2 amp.original)
2 amp.original) /2, AA =
/2, AA =  /2, AN =
/2, AN = /4
/4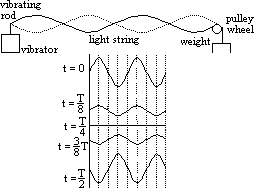
 /2 => f0 = v/
/2 => f0 = v/ = v/2l
= v/2l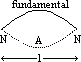
 1 => f0 = v/
1 => f0 = v/ 1 = v/l = 2f0
1 = v/l = 2f0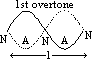
 1/2 => f0 = v/
1/2 => f0 = v/ 2 = 3v/2l = 3f0
2 = 3v/2l = 3f0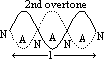
| closed | open | |
| fundamental freq, f0 (1st harmonic) | l = /4 => f0 = v/ /4 => f0 = v/ = v/4l = v/4l |
l = /2 => f0 = v/ /2 => f0 = v/ = v/2l = v/2l |
| 1st overtone, f1 (2nd harmonic) | l =3 1/4 => f1 = v/ 1/4 => f1 = v/ 1 = 3v/4l = 3f0 1 = 3v/4l = 3f0 |
l = 1 => f1 = v/ 1 => f1 = v/ 1 = v/l = 2f0 1 = v/l = 2f0 |
| 2nd overtone, f2 (3rd harmonic) | l =5 2/4 => f2 = v/ 2/4 => f2 = v/ 2 = 5v/4l = 5f0 2 = 5v/4l = 5f0 |
l =3 2/2 => f2 = v/ 2/2 => f2 = v/ 2 = 3v/2l = 3f0 2 = 3v/2l = 3f0 |
| nth overtone | (2n+1)f0 | (n+1)f0 |
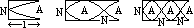
| 
|
 of sound using stationary waves
of sound using stationary waves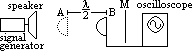
 /2 =>
/2 =>  = 2x
= 2x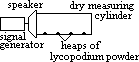
 /2
/2
 /4
/4 /4
/4 /2
/2