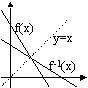Amaths1
SURDS-irrational roots
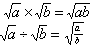
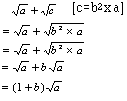
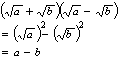
INDICES
a0 = 1
am × an = am+n
an × bn = (ab)n
(am)n = amn
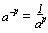
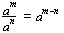
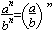
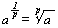
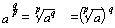
LOGARITHMS
ab = C (index form) 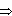 logaC = b (logarithmic form) C>0,a>0,a1
logaC = b (logarithmic form) C>0,a>0,a1
loga xy = logax + logay
loga (x/y) = logax - logay
loga xn = n logax
loga a = 1
loga 1 = 0
lg = log10
lg C = b  10b = C
10b = C
loge x = ln x
eb = C  ln C = b
ln C = b
ln xy = ln x + ln y
ln (x/y) = ln x - ln y
ln xn = n ln x
ln e = 1
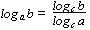
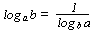
ax = b, (b = an) 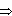 ax = an > x = n (a
ax = an > x = n (a 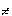 -1,0,1)
-1,0,1)
QUADRATIC EQUATIONS: ax2 + bx + c = 0
Discriminant = b2 - 4ac
b2 - 4ac > 0  real and distinct roots
real and distinct roots
b2 - 4ac = 0  real and equal roots
real and equal roots
b2 - 4ac < 0  no real roots
no real roots
y = ax2 + bx + c
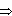 a(x - a)(x - b) [turning point.: x = (a+b)÷2]
a(x - a)(x - b) [turning point.: x = (a+b)÷2]
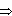 a(x - h)2 + k [(h,k) = turning pt.]
a(x - h)2 + k [(h,k) = turning pt.]
a < 0 max.pt., a > 0 min. pt.
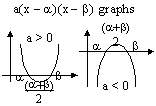
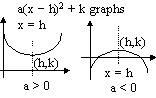
(x - a)(x - b) < 0  a < x < b
a < x < b
(x - a)(x - b) > 0  x < a or x > b
x < a or x > b
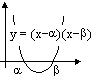
REMAINDER THEOREM
f(x) divided by (x - a) > remainder = f(a)
FACTOR THEOREM
(x - a): factor of f(x) > f(a) = 0
CUBIC EQUATIONS
px3 + qx2 + rx + s = 0  (x - a)(ax2 + bx + c) = 0 [s
(x - a)(ax2 + bx + c) = 0 [s  0, (x - a) = a factor)]
0, (x - a) = a factor)]
COORDINATE GEOMETRY
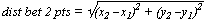
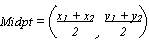
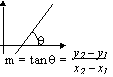
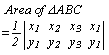
= ½(x1 y2 + x2 y3 + x3 y1 - y1 x2 - y2 x3 - y3 x1)
[A = (x1, y1), B = (x2, y2), C = (x3, y3), pts. taken in anti-clockwise direction]
Equation of a straight line
y - y1 = m(x - x1) [(x1, y1) lines on line]
Parallel lines
y = m1x + c1 & y = m2x + c2 are parallel  m1 = m2
m1 = m2
Perpendicular lines
y = m1x + c1 & y = m2x + c2 are perpendicular, m1m2 = -1
LINEAR LAW
Y = mX + c [m & c = constant, Y & X = variables]
FUNCTIONS
f : x  x + 1
x + 1  f(x) = x+1
f(x) = x+1
Finding the Inverse Function
f : x 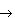 x + 1: Let f(x) = y
x + 1: Let f(x) = y 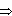 y = x + 1
y = x + 1 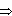 Make x the subject
Make x the subject 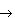 x = y-1
x = y-1  f -1 : x
f -1 : x  y-1
y-1
gf(x)= g(f(x))
(gf)-1 = f-1g-1
f-1f(x) = ff-1 (x) = 1
In graphs, f-1(x) = reflection of f(x) in the line y = x
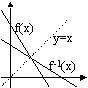
ABSOLUTE VALUES
|x| = absolute value of x (numerical value)
| ±x |= x
Amaths2
Amaths3
Amaths4
Amaths5
Back to notes index
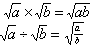
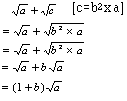
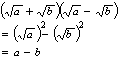
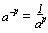
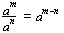
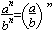
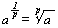
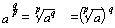
 logaC = b (logarithmic form) C>0,a>0,a1
logaC = b (logarithmic form) C>0,a>0,a1 10b = C
10b = C ln C = b
ln C = b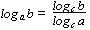
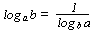
 ax = an > x = n (a
ax = an > x = n (a  -1,0,1)
-1,0,1) real and distinct roots
real and distinct roots real and equal roots
real and equal roots no real roots
no real roots a(x - a)(x - b) [turning point.: x = (a+b)÷2]
a(x - a)(x - b) [turning point.: x = (a+b)÷2] a(x - h)2 + k [(h,k) = turning pt.]
a(x - h)2 + k [(h,k) = turning pt.]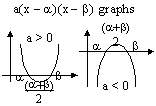
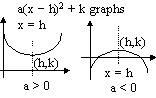
 a < x < b
a < x < b x < a or x > b
x < a or x > b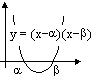
 (x - a)(ax2 + bx + c) = 0 [s
(x - a)(ax2 + bx + c) = 0 [s  0, (x - a) = a factor)]
0, (x - a) = a factor)]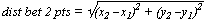
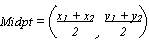
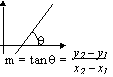
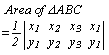
 m1 = m2
m1 = m2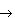 x + 1
x + 1  f(x) = x+1
f(x) = x+1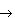 x + 1: Let f(x) = y
x + 1: Let f(x) = y  y = x + 1
y = x + 1  Make x the subject
Make x the subject  x = y-1
x = y-1  f -1 : x
f -1 : x  y-1
y-1