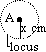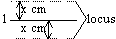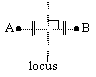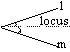Emaths2
Statistics
| class | class width | freq | mid values | freq density | cumulative freq
|
|---|
| 50 - 59 | 10 | 5 | 54.5 | 2.5 | 5
|
| 60 - 64 | 5 | 2 | 62 | 2 | 7
|
| 65 - 68 | 4 | 4 | 66.5 | 5 | 11
|
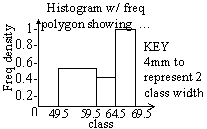
Lower class limit: 50, 60, 65, upper class limit: 59, 64, 68
True class limits/ class boundaries = ±0.5 + class limit
Class width = upper class boundary - lower class boundary
Freq density = freq class width
Freq polygon: used mid-values
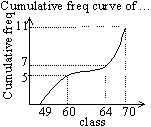
Cumulative freq: use upper class limit to plot pts
Mean = sum of fX total freq (f = freq for a group, X = midpt for a group-grouped data / class)
lower quartile: class corr. to of cum. freq, upper quartile: class corr. to of cum. freq
inter-quartile range: upper - lower quartile, percentile: class corr. to x% of cum. freq
(25th percentile = lower quartile, 75th percentile = upper quartile, 50th percentile = median)
Variation
| y is proportional to x | y is inversely proportional to x
|
|---|
| y ∝ x | y ∝ 1/x
|
| y = kx, k = constant | y = k/x, k = constant
|
Transformation
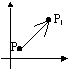
P is mapped onto P1 under a transformation U  U(P) = P1
U(P) = P1
Reflection
P is mapped onto P1 under a reflection in the line, l
Rotation
P is mapped onto P1 under a clockwise rotation of x about C
Translation
P is mapped onto P1 under a translation of translation vector 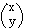
Enlargement
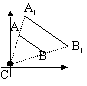
AB is mapped onto A1B1 under an enlargement of scale factor, k w/ a centre of enlargement, C, k = length of (image/object) or length of (AC/A1C) (k: -ve > image & object on opp sides of C)
Shear
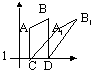
ABCD is mapped onto A1B1CD under a shear w/ shear factor, k and l as the invariant line, k = dist bet (A and A1/A and invariant line) (AA1 // l) (k: +ve > up and right, k: -ve > left and down)
Stretch
ABC is mapped onto ABC1 under a stretch w/ stretch factor, k and invariant line, l, k = dist bet (C & l/ C1 & l)
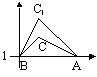
Combination of transformations
Transformation XY = transformation (Y > X)
Matrix representation of transformations
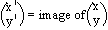
Translation, T: object + translation vector = image

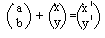
Reflection, rotation, enlargement, shear, stretch: pre-multiply
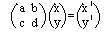
Vectors
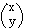
x = horizontal dist, y = vertical dist
right/up: +ve, left/down: -ve
equivalent vectors: same magnitude & direction
-ve sign reverses direction of vector
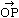 = c = c
= c = c
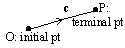
zero vector (a pt) = 0 = 0 =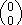
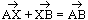
Position vector of P (x, y), where O is origin
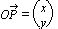
ka = vector parallel to a, same direction, k times magnitude of a
-ka = vector parallel to a, opposite direction, k times magnitude of a
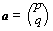
magnitude of a = |a| = 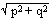

A, B, C are collinear 

Probability
Probability of (E), P(E) = n(E) / n(S)
n(E) = # of favourable outcomes, n(S) = # of possible outcomes (sample space)
0  P(E)
P(E)  1, P(E) + P(E') = 1
1, P(E) + P(E') = 1
Possibility diagram
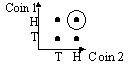
P(both heads) = ¼
Tree diagram
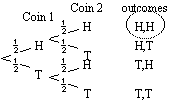
P(both heads) = ½ × ½ = ¼
A & B: mutually exclusive events: A & B cannot occur at once
p(A or B occurring) = p (A 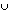 B) = p(A) + p(B)
B) = p(A) + p(B)
To find probability of 2 or more events happening together using a tree diagram
-determine if probability of outcome is affected by previous event
-calculate respective probabilities along branches of tree diagram
-multiply probabilities along relevant branches
Loci
2-D loci
Locus of a pt x cm from given pt A = a circle w/ radius of x cm & A as the centre
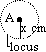
Locus of a pt x cm from given line, l = parallel lines on both sides of l and each x cm from l (& same length of l)
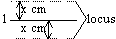
Locus of a pt equidistant from 2 given pts, A & B = perpendicular bisector of line segment AB
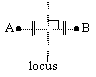
Locus of a pt equidistant from 2 given intersecting lines, m & l = a pair of perpendicular lines bisecting the angle's bet l & m
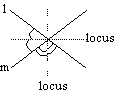
Locus of a pt equidistant from 2 given touching lines, l & m = bisector of the angles(s) bet l & m
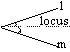
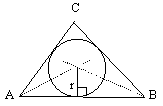
To draw an incircle/ inscribed circle of triangle ABC
-draw 2 loci of pts equidistant from 2 different pairs of 2 sides of the triangle
-draw perpendicular from a line passing through the pt of intersection, perpendicular = radius of circle
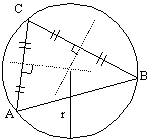
To draw a circumscribed/ circumcircle of triangle ABC
-draw perpendicular bisectors of 2 sides
-draw the circle w/ pt of intersection of loci as centre of circle
3-D loci
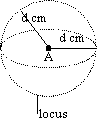
locus of a pt d cm from given pt A = SA of a sphere w/ A as the centre & a radius of d cm
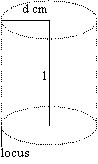
locus of a pt d cm from given line l = curved surface or a cylinder w/ l as its axis & a radius of d cm
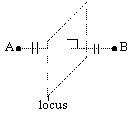
locus of a pt equidistant from 2 given pts, A & B = a plane perpendicular to & bisecting line segment AB
Emaths1
Back to 'O' level notes index
Back to notes index


 U(P) = P1
U(P) = P1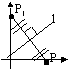

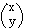



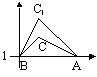
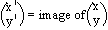

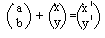
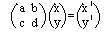
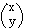
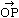 = c = c
= c = c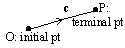
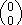
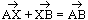
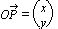
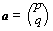
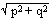



 P(E)
P(E)  1, P(E) + P(E') = 1
1, P(E) + P(E') = 1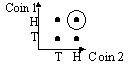
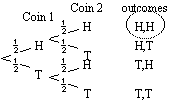
 B) = p(A) + p(B)
B) = p(A) + p(B)