OSCILLATIONS
oscillating/periodic motion: motion repeated over & over in a regular cycle

frequency of motion, ƒ: # of times motion repeated in 1 second (hertz, Hz, ie s^-1)
period, T: time for 1 complete oscillation (T = 1/ƒ)

Simple harmonic motion
-a periodic motion where obj moves back & forth regularly over the same path

-middle of path of motion = equilibrium position (position of rest if obj hung and left to rest)

-greatest dist mover from equilibrium position = amplitude of motion, A

Conditions of SHM
a ∝ -kx [k: +ve constant => a ∝ -ω²x]
-acceleration directly proportional to displacement from equilibrium position
-acceleration always directed towards equilibrium position (shown by -ve sign) [=>a restoring force acting towards equilibrium position (SHM differs from other forms of motion as F changes during cycle)]

max speed; x = 0 (at equil^m pos) => a = 0 => F = 0
min speed; x = ±A => |a| = max => |F| = max

A hydrometer made from a weighted rule shows SHM and can be used to measure liquid density form liquid level on scale

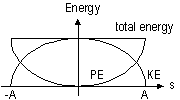
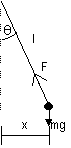
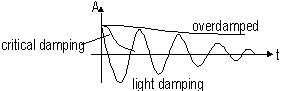
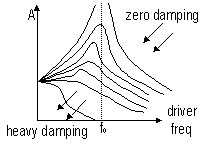
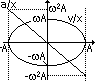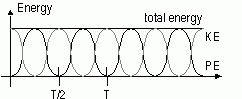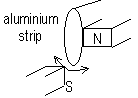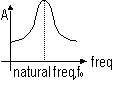for oscillation where at time = 0, x = 0	for oscillation where at time = 0, x = ±A
x = A sin(ωt) = A sinθ	x = A cos(ωt) = A cosθ
v = dx/dt = Aω cos(ωt) = Aω cosθ	v = dx/dt = -Aω sin(ωt) = -Aω sinθ
a = dv/dt = d2x/dt2 = -Aω2 sin(ωt) = -Aω2 sinθ	a = dv/dt = d2x/dt2 = -Aω2 cos(ωt) = -Aω2 cosθ

x = A sinθ => x² = A² sin²θ => sin²θ = x²/A²
v = ωA cosθ => v² = ω²A² cos²θ => cos²θ = v²/(ω²A²)
sin²θ + cos²θ = 1
x²/A² + v²/(ω²A²) = 1
v² = ω²A² - ω²x²
v = ±ω √(A² - x²)

a = -Aω² sinθ, x = A sinθ => a = -ω²x


Energy in SHM
v = ±ω √(A² - x²)
KE = ½ mv² = ½ mω²(A² - x²)

KE = ½ mv2 = ½ mω²A²cos²(ωt)



Prove a motion is SHM
show: a = -ω²x


taking right as positive
F cosθ = mg
F sinθ = -ma
for v.small θ: cosθ ≈ 1, sin θ ≈ x/l
∴F = mg, F x/l = -ma
∴ mgx/l =-ma
=> a = -(g/l) x
for a system: g & l are +ve constant => g/l = +ve constant ∴ a = -ω²x
ω² = g/l => ω = √(g/l)
T = 2π /ω = 2π√(l/g)

Damping
damping = effect where in real SHM: amplitude of motion decrease to 0, due to loss of energy
damping due to viscous forces; friction, air resistance, liquid viscousity (energy > heat)
for damping

-oscillation period is constant (T = constant) (only for light damping)
-after each cycle: decrease of same proportion (water: 40%, air: 10%)
-dotted line joining max pts of displacement = decay envelope (exponential curve)

due to damping pendulum clocks need energy (wound up spring, batteries,..) to replace energy loss due to damping in order for its amplitude to remain constant

damping- reduces unwanted oscillations (in elec meters: heavy damping- pointer stops quickly, cars: shock absorbers)
w/ magnets: eddy currents induced on Al strip when moving > opposing F which damps movement
w/o magnets: less damping (no eddy currents) > oscillates more

damping ^: T ^
-damping ^ more: enough F to just prevent system vibrating past equil. pos
(ie. critical damping: reduces motion to in min time)
-damping ^ even further: overdamped- no vibrations occur, system takes long time to settle to rest



Forced oscillation: occurs when a free to move obj oscillates due to repeated varying external force
[freq of obj motion = freq of driving F]
Resonance: if driving force matches natural freq of system > amplitude increases greatly (to ∞) [other freq: smaller A]
useful: musical instruments, radio receivers (buildings + bridges: designed so seismic vib/wind doesn't cause resonance)



Types of oscillation
-in phase: T₁ = T₂, A₁ =/≠ A₂, start oscillating at same time (max, min + zero disp of both oscillations occur at same time)
-out of phase: oscillations start at different times
-anti-phase: oscillations moving in opposite dirⁿs, T₁=T₂ (π rad out of phase)


Back to 'A' level notes index

Back to notes index