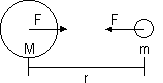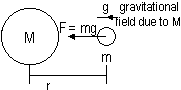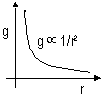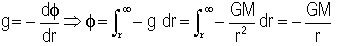GRAVITATION
gravitational field: region (3-D) where a gravitational F is experienced

Newton's Law of gravitation: 'Every particle of matter in the universe attracts each other particle w/ a gravitational F that is directly proportional to the product of the masses of the particles and inversely proportional to the square of the dist bet them'

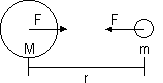
F ∝Mm/r²
  => F = GMm/r²
[G = gravitational const: 6.672 x 10^-  11Nm²/kg²,
  r = dist bet obj,
  m = mass of small obj,
  M = mass of massive obj, eg Earth, Sun]

Newton's law: eg. for an inverse square law

Gravitational forces: -always attract, -v.v.weak (unless at least 1 obj of planetary mass or more)

Gravitational field strength, g (at a pt) = gravitational F per unit mass (acting at that pt)

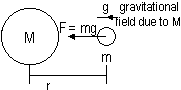
g = F/m
g: vector, variable (near Earth surface ~const: v.v. small change => assumed const, 9.81N/kg)

F = GMm/r²
g = F/m = GMm/mr² = GM/r²
[M = mass of other,massive obj => 'g' doesn't depend of mass of obj, m]

Earth gravitational field strength

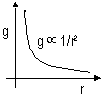
at Earth surface: g₀ = GM/R² [M = mass of Earth, R = radius of Earth]
above Earth surface: g = GM/r² [r = dist from Earth centre]
GM = g₀R²
g = GM/R²
  => g = g₀R²/r² => dist from Earth ^, g decreases
at Earth's centre: g = 0: mass pulled equally in all dirⁿ => F_R = 0

GPE: WD bringing obj from infinity to pt (dist r from centre of big mass, M) (depends on mass)

Gravitational potential (at a pt): WB bringing a unit mass from infinity to pt (dist r from M)
φ/V = W/m = GPE/m
at infinity: V = 0, elsewhere: v = -ve
gravity = F of attraction, WD by mass as it moves from infinity > pt


If Δr is v.v.small: uniform field > F ~const (same dirⁿ + mag)> g ~const (F=mg)
ΔW = -FΔr
F = mg => ΔW = -mgΔr [work done is -ve as it is done by obj]
ΔV = ΔW/m => ΔV = -gΔr => g = -ΔV/Δr [uniform field]
non-uniform field: g = - dV/dr

g = GM/r²


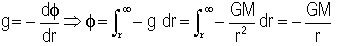
g₀ = GM/R²
V = -GM/r
V = -g₀R²/r (r = dist bet 2 obj)
[V₀ = -g₀R (R = radius of Earth)]

Escape speed, v_esc: speed at which obj must leave a planet's surface in order to escape the gravitational field (obj > ∞)
loss KE = gain PE
½ mv² - 0 = 0 - (-GMm/R)
  => v² = 2GM/R
F = mg = GMm/r²
  => g₀ = GM/R²
  => GM/R = g₀R
  => v² = 2g₀R

Circular orbits
centripetal F provided by gravitational F:
 F = mv²/r = GMm/r²
  => v² = GM/r (speed only depends on radius + M, not 'm')
g₀ = GM/R² (R = Earth's radius)
  => GM = g₀(R)²
  => v² = g₀(R)²/r

F = GMm/r² = mω²r
  => GM/r³ = ω² = (2π/T)² = 4π ²/T²
  => T²/r³ = 4π ²/GM
  => T² = (4π ²/GM) r³
  => T² = k r³
  => T²∝ r³ (T ∝ r^1.5; r ^,T ^)
4π ²/GM: const for all obj orbiting large mass M (=> T²/r³ = const)
Kepler's 3^rd Law: T² ∝ r³ (T:T of planet, r: dist from Sun)

Geostationery orbit: orbit w/ T = T of Earth's rotation = 24h
-satellite appears stationery in sky, same place at all times (rel to pt)
-easy to relay info bet satellite & Earth

Weightlessness: due to person & floor moving w/ equal acc (same mag. + dirⁿ)
-contact F w/ floor = 0N (same if in zero gravity)


Back to 'A' level notes index

Back to notes index