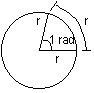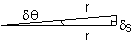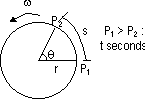CIRCULAR MOTION

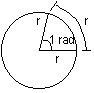
1 radian = 1 rad = 1^C = angle when arc = radius
radian: dimensionless


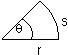
θ = angular displacement
θ =s/r
1 revolution: θ = 2πr/r = 2π rad = 360° => 1 rad ≈ 57.3°

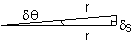
δθ: v. small angle => δs considered st. line perpendicular to radius at start
sin δθ = δs/r = δθ => for v.small angles: sin δθ = δθ

Angular velocity, ω (rad/s or s^-1): rate of change of angular displacement (angle turned per unit time)
const speed:
 ω = θ
     t
varying speed: ω = dθ/dt

Frequency, ƒ (hertz, Hz): rate of rotation
ƒ = # of rotations/time

Period, T (s): time for 1 revolution
T = ƒ ^-1

for 1 revolution: ω = θ/t = 2π/T = 2πf


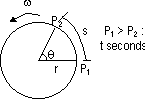
const speed: v = s/t [v= linear vel]
θ = ωt = s/r => s = ωtr
v = ωtr/t = ωr
linear vel = angular vel x radius: const speed
v = ωr

Centripetal acceleration: movement in a circle w/ uniform speed but changing vel, due to centripetal F acting towards centre of circle (F moves obj in circle, since F perpendicular to vel => doesn't change speed, only dirⁿ)
const speed: a = v²/r = ω²r
F = ma => F = mv²/r = mω²r


Back to 'A' level notes index

Back to notes index