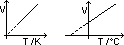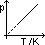IDEAL GAS
GAS LAWS(T- temp/K, p- pressure/Pa, V- vol/m₃)
Boyle's law
T const => p ∝ 1/V (const mass)
pV = k


Charles's law
p const => V ∝ T (const mass)
V/T = k


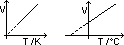
Pressure law
V const => p ∝ T (const mass)
p/T = k


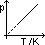
general gas law/ eqn of state: pV/T= k
-accurate for low pressure (high pressure: gas behaviour deviates)
-concept of ideal gas derived => ideal gas obey eqn under all conditions
Ideal gas eqn; pV/T = k => p₁V₁/T₁ = p₂V₂/T₂
pV/T ∝ n (n: # of moles) => pV/T = nR (R = molar gas const)
pV = nRT
n = (N/N_A)RT
R/N_A = k = Botlzman's constant (gas const for individual molecule)
pV = NkT
Assumptions of kinetic theory of gases
-any gas consists of a v.large # of molecules
-molecules of gas in rapid, random motion
-collision of gas molecules w/ each other and walls of container are perfectly elastic
-intermolecular forces of attraction are negligible
-duratn of collision negligible compared to time interval bet collisions
-vol of gas molecules negligible compared to vol of container
Kinetic calculation of pressure

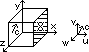
cube of side l containing N molecules
-each molecule: -mass, m, -velocity at any intstant, c
c resolved into u, v, w (components in x, y, z dirn)
c² = u² + v² + w²
considering x-component, u
F exerted by face X during collision
momentum change on impact = mu - (-mu) = 2mu
time bet collisions w/ face X = 2l/u
freq of collisions w/ face X, n' = 1/(2l/u) = u/2l
at X: momentum change per second = F (Newton's 2nd law)
        F = n' × momentum change per collision = u/2l × 2mu = mu²/l
pressure on X = F/A = (mu²/l)/l² = mu²/l³ = mu²/V
each molecule diff vel => diff mag of compenent in x dirn, u₁, u₂,.., u_n
p = m(u₁² + u₂² + .. + u_n²)/V
<u²> = (u₁² + u₂² + .. + u_n²)/N
p = Nm<u²>/V
since large # of molecules => <u²> = <v²> = <w²>
<c²> = <u²> + <v²> + <w²>
<u²> = <c²>/3
<c²> = mean square speed
p = Nm<c²>/3V
pV = Nm<c²>/3
pV: macroscopic
Nm<c²>/3 : microscopic
Nm/V = M/V = denisity, ρ
p = ρ<c²>/3
rms speed, c_rms = √<c²> = √ [(c₁² + c₂² + .. + c_n²)/N]
p = ρ<c²>/3 => c_rms represents av speed of all molecules to define a particular state (giving rise to a particular pressure at a particular temp)
p = (M_m/V_m)<c²>/3        M_m: molar mass, V_m: vol of 1 mole of gas
pV_m = M_m<c²>/3 = RT (n = 1) => <c²> = 3RT/M_m
c_rms = √(3RT/M_m)
  pV = NkT
  pV = Nm<c²>/3
kT = m<c²>/3 => KE = m<c²>/2 = 3kT/2
av KE of translation of molecules ∝ T (T: abs temp, K)


Back to 'A' level notes index

Back to notes index