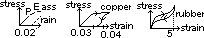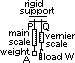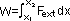DEFROMATION OF SOLIDS
stress: F acting on unit cross-sectional area, A
stress = F/A [Pa/Nm^-2]
-increase length > tension, tensile stress
-decrease length > compression, compressive stress
strain: extension per unit length
strain = e/l [e: extension, l: original length]

general stress-strain graph of ductile material (OPEAD) (ductile- long deformn before break, ie large plastic region)

elastic deformn:
-OP st. line through (0,0) => strain directly proportional to stress [e/l ∝ F/A => F ∝ e (l, A: const for given wire)] [P: proportional limit]
-OP > E (elastic limit): strain not proportional to stress (non-linear graph), but still returns to original length when stress removed
plastic/ permanent deformn:
-occurs beyond E; when stress removed > permanent extension
-small increase in stress > large increase in strain
-if load removed at A, recovery of wire along AO' (almost // to OP) > OO' => permanent extension; stress reapplied O'AD
at D: more than 1 'waists' form (material becomes very thin) => ductile fracture occurs at one
stress at D = greatest stress material can bear = breaking stress


graph OB: for brittle material (glass, concrete)- fractures almost immediately after elastic stage > little/ no plastic deformation


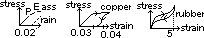
rubber: -can stretch 5 times ori length, -diff on loading & unloading

Young modulus: ratio of tensile stress to tensile strain (within proportionality limit)
Young modulus of elasticity, E = tensile (stress/strain) = (F/A)/(e/l) = Fl/Ae [Pa]
for a wire; ext increase: F increase, A decrease (thinner), l increase (longer), E decrease [e = Fl/AE]

Determining Young's modulus

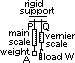
P,Q: 2 wires of same length & material (straight wires free from knots/ twists which affect extension)
use 2 wire to compensate for -sagging of support, -temp change
wire: (1)thin- larger stress > larger extn, (2)long- smaller error in extn measured (long extn)
(1)load W loaded > extn measured by vernier (extn small > reduce error) [original length of wire ~2m measured by metre rule]
(2)readings taken on unloading > check proportional limit not exceeded
(3)plot F-e graph [through origin]

(4)micrometer screw gauge used to measure diameter of wire at several places > average found
E = (F/A)/(e/l) = (F/e) × (l/A) [F/e = grad of F-e graph since through origin]
[creep: time weight loaded increase > extn increase]
Strain energy in deformed material

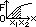
energy needed to stretch a wire
when stretched: PE lost store in wire as strain E
if elastic lmt not exceeded: energy fully recoverable on unloading
if elastic lmt exceeded: some energy used to permanently deformed wire (crystal slip in wire maintained > permament extn)
external F causing wire to extend from x₁ > x₂
WD = strain energy = area under F-e graph

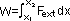
Hooke's law obeyed: W = ½Fx = ½kx² => strain energy = ½kx²
for wire of length,l, & area,A => vol = lA
strain per unit vol = ½Fe/(Al) = ½(stress × strain)


Back to 'A' level notes index

Back to notes index