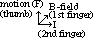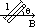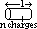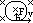MAGNETIC FIELDS mag field: space around a magnet where a mag F is experienced
dirⁿ of field given by dirⁿ of F on N mag pole at that pt
represented by mag field lines such that
-lines (or tangent to curve) gives dirⁿ of field at that pt
-# of lines per unit cross-sectional area indicates 'strength' of field
field lines: obtained by Fe filings/ compasses


Force on current-carrying conductors in a magnetic field
I-carrying conductors in a mag field due to another source will experience a mechanical F
dirⁿ of F given by Flemings left-hand rule (motor rule)


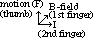
if cond makes an angle of θ with B-field => F = BIlsinθ


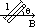
magnetic flux density, B: F acting per unit I in a wire of unit length at right angles to the field
B = F/Il 1 tesla = 1T = mag flux density of a universal field when F on 1m long cond, placed perpendicular to field and carrying 1A of I, is 1N
Measurement of mag flux density using a current balance

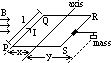
light rectangular coil PQRS connected to DC => current, I, flow in & out through axis

PQ perpendicular to B-field => F_down on PQ = BIl
mass moved until equilibrium
BIlx = mgy => B = mgy/Ilx
Mag field of current-carrying conductor
-use right hand grip rule (thumb: dirⁿ of current, fingers: dirⁿ of field)

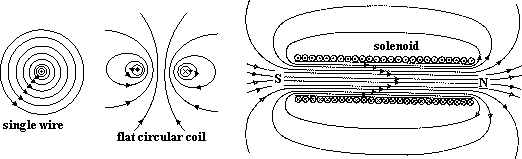
Effect of ferrous core on field due to solenoid
when Fe rod place in solenoid > increase mag flux density (field lines conc in region)
DC passed through coil wound around soft iron > iron becomes temp electromagnet
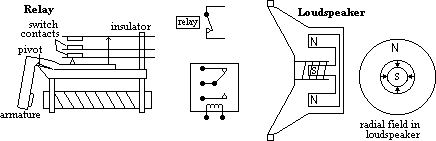
uses of electromagnet: door bell, pick up scrap iron, railways, Reed switch, loud speaker


Force on charge moving in a mag field
elec I = flow of charge > F experience by I-carrying cond in B-field = resultant F on charges

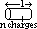
each charge = Q, drift vel = v, # of charges in length l = n
time, t such that v = l/t > t = l/v
total charge passing any cross section in time t = nQ
I = charge flowing / time = nQ/t = nQv/l
if cond makes angle θ w/ B-field, F = IlBsinθ = (nQV/l)lBsinθ = nQvBsinθ (F on n charges)
F on a charge = nQvBsinθ/n = QvBsinθ
F = QvB (for field & path perpendicular )

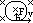
F: perpendicular to field & path of particles > change on dirn not speed > circular path
F = centripetal F = mv²/r = BQv > r = mv/BQ

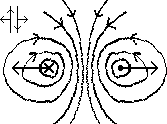
Force bet current-carrying conductors
current-carrying conductors near each other exert a F on each other
'like currents attract, unlike currents repel'

use mag field lines / Fleming's LHR
mag field lines:-
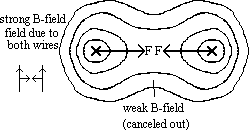
currents in same direction:
-in bet wires: mag field of each wire cancels each other > weak field
-on outside of wire: mag field of both wires same direction > stronger field
-resultant inwards F

currents in opposite directions:
-in bet wires: mag field of both wires same direction > stronger field
-on outside of wire: mag field of each wire cancels each other > weak field
-resultant outwards F


Fleming's LHR
-consider current in one wire w/ mag field of other wire
-Newton's 3^rd law > opposite & equal force on other wire
currents in same direction: -inwards F
currents in opposite directions: -outward F

Hall effect: emf set up across I-carrying conductors when there is a perpendicular B-field

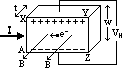
F_down on electrons (F= BvQ) > electrons accumulate on lower side > AZ –ve charge & lower potential w/ respect to XY > pd /emf opposes electron movement > at particular emf, Hall voltage, V_H > flow stops
elec F = mag F
eE = Bev > E = Bv [I = nave > v = I/nAe]
E = V/x = V_H/w = BI/nAe > V_H = BIw/nAe = BIw/ntwe = BI/net
V_H = BI/net
V_H: small for metals (n: v.large), large for semi-conductors (n: v.small)
calibrated Hall probe: measures mag field density, B


Back to 'A' level notes index

Back to notes index