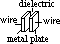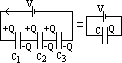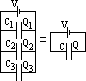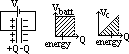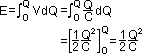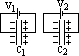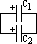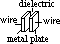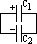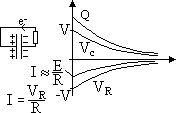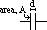CAPACITANCE

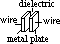
capacitor: stores electric charges for release later

parallel plate capacitor: made of 2 parallel metal plates separated by insulating medium (dielectric; could be mica, paper, oil, air)
capacitors: plate & dielectric rolled up > save space

capacitors in electronic circuits -tuning circuit (TV, radio), -flashing untis (car indicators, camera flash lights), -control units for air-conditioners, -power supply units (AC > DC)


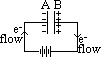
capacitor charged by connecting leads to battery terminal
> electrons flow > accumulate on one plate (A)
> attracts same # of electrons (accumulated at A) from other plate (B)
> plates of opposite charge w/ same magnitude (same # of protons & electrons)
fully charged capacitor
-electron flow stops (no I)
-plates of equal & opposite amt of charges
-pd across plates, V = supply voltage
-electric field bet plates, E = V/d

capacitance, C: amt of charge a capacitor can store when connected across pd of 1V
C = Q/V (F; farad = coulomb/volt, C/V)
1 F = 1 C/V
capacitor's max voltage exceeded > dielectric may fail > ruin capacitor

capacitors in series

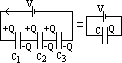
V = V₁ + V₂ + V₃
Q/C = Q/C₁ + Q/C₂ + Q/C₃
1/C = 1/C₁ + 1/C₂ + 1/C₃
C = (Σ C_i^-1)^-1
(conservation of charges; C₁, C₂, C₃: same charge, diff pd)

capacitors in parallel

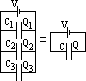
Q = Q₁ + Q₂ + Q₃
CV = C₁V + C₂V + C₃
C = C₁ + C₂ + C₃
C = Σ C_i
(same pd since parallel, diff charge)

Energy stored

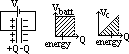
E_supplied = QV
E_stored = ½QV = ½CV² = ½Q²/C


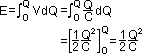
other ½QV lost as heat in resistances


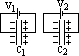
C = Q/V => Q₁ = C₁V₁, Q₂ = C₂V₂
C₁ & C₂ joined > chares redistributed until pd across C₁ & C₂ are equal
(1)+ve to +ve

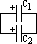
Q = CV
Q₁ + Q₂ = (C₁ + C₂)V
C₁V₁ + C₂V₂= (C₁ + C₂)V
V = (C₁V₁ + C₂V₂)/(C₁ + C₂) = (Q₁ + Q₂)/(C₁ + C₂)

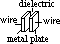
V = Σ Q/Σ C
(2)+ve to -ve; Σ Q = |Q₁ - Q₂|

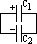
+ve to -ve; more energy lost due to less net charge (neutralised)

Charging capacitors

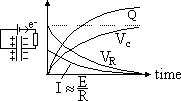
initial: V_C = 0, V_R = 0
switch on: capacitor charges; at first big current
> pd_C increases > this increase slows down as pd_C opposes V_battery
C = Q/V_C => Q = CV_C => Q increases w/ V_C

V_C+ V_R = V ∝E
I = V_R/R => current decreases to 0

Discharging capacitors

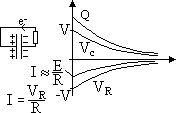
V_C = -V_R => V_C + V_R = 0

Effect of plate distance and different dielectrics on capacitance

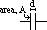
C ∝ A/d => C = εA/d
E = ½QV = ½CV² = ½Q²/C
-plates moved closer w/ batt connection: C increases (more charge stored, pd constant as still connected to batt) => E increases (½QV)
-plates moved closer w/o batt connection: C increases => E decreases (½Q²/C)
-dielectric inserted w/ batt connection: C increases, V constant => E increases (½CV²)
-dielectric inserted w/o batt connection: C increases, Q constant => E decreases (½Q²/C)


Back to 'A' level notes index

Back to notes index