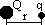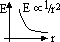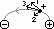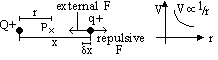ELECTRIC FIELD

Coulomb's law: F bet 2 pt charges Q₁ & Q₂ is proportional to each of the charge & inversely proportional to dist bet pts

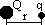
F ∝Q₁Q₂/r² => F = kQ₁Q₂/r² = F = Q₁Q₂/(4πε₀r²)
k = 1/4πε₀, ε₀ = permittivity of free space = 8.85 × 10^-12C²N^-1m^-2 (F/m- Farad/metre), ε_air = 1.0005ε₀

electric field = region where electrostatic F is experience by a charge
electric field strength at a pt, E = F per unit +ve charge at pt
-a vector, direction = direction of F
E = F/q (N/C) = Qq/(4πε₀r²)(q) = Q/(4πε₀r²) [Q: charge of other body]



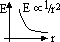
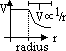
electric field of sphere w/ charge uniformly distributed on surface
-identical if pt charge at sphere centre, provided r > radius (inside sphere: E diff)

electric field stength
around dipole (dipole: a pair of charges- equal mag, opp signs)
-found by scale drawing
(1)find E due to (i)+ve on test charge, (ii)-ve on test charge
(2)find resultant E at pt

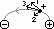
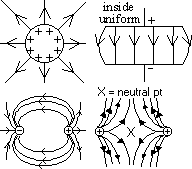
inside charge conductor
-if no current in conductor > no F for electrons to drift > no electric field
inside hollow conductor
-zero charge on inside surface of sphere & zero field within hollow sphere
-charge placed inside hollow conductor immediately flows to outside surface > inside 0 field (important in Van de Graaf generator & Faraday's cage)

electric potential at a pt in an electric field, V = WD in moving unit charge from infinity to the pt (infinity: a pt far away from all other electrical influence)
V = W/q (J/C = V- volt)


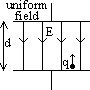
E = F/q => F = Eq
W = Fd = Eqd (WD in moving charge against field at const vel)
[if WD in direction of field > -ve work]
W = Eqd => W/q = Ed => V = Ed

E = V/d (for uniform field: pd per unit dist = electric field)
dirⁿ of E = dirⁿ of decreasing potential (high > low, +ve > -ve)
non-uniform field: small charge, q, moves small dist, δx (A > B) > work = δW

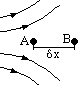
since small dist > E ~ const: δW = -qEδx => δV = -Eδx => E = -δV/δx, x → 0, E = -dV/dx

electric potential gradient = electric field strength (dirⁿ of field = dirⁿ of decreasing potential)


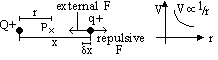
WD by external system in moving δx: δW = -Fδx = -qEδx
WD by external system moving q from ∞ to P:


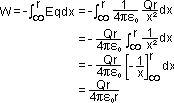
charge sphere; on surface & inside: E = 0 = -dV/dx => V const

	Gravitational	Electrostatic
(inverse square law)	F ∝ 1/r2	F ∝ 1/r2
(F ∝ property)	F ∝ m	F ∝ q
	attractive F only	attractive/ repulsive F
potential:	W/m	W/q
field strength:	F/m	F/q
	independent of medium	depends on medium(εx)

Back to 'A' level notes index

Back to notes index