DC CIRCUITS
Kirchhoff's 1st law: algebraic sum of current at a junction is zero, Σ I = O

-at any junction: total I flowing in (+ve I) = total I flowing out (-ve I)
-statement of conservation of charge
Kirchhoff's 2nd law: around any closed circuit (loop), algebraic sum of all emfs = algebraic sum of pds
Σ ζ = Σ IR (for resistive circuit)

-statement of conservation of energy
-each pt in a stable electrical circuit: has particular potential provided a charge returns to original position w/o any energy gain/loss (ie when going round circuit: elec E gained = elec E loss, no matter path taken)
-externally(conventional current): +ve > -ve: high > low potential , internally(electron movement): -ve > +ve
-if pds is +ve: same dirⁿ as net emf

Equivalent resistance
Resistors in series

K 1st law: I- equal for all resistors
V =IR => V_T = V₁ + V₂ + V₃ = IR₁ + IR₂ + IR₃ = I(R₁ + R₂ + R₃)
R = V_T/I = R₁ + R₂ + R₃ [R > R_max<1,2,3>> R_individual]
R_T = Σ R (for series connection)

Resistors in parallel

K 1st law: I = I ₁ + I ₂ + I ₃
K 2nd law: V_T = V₁ + V₂ + V₃
V/R = I => V_T/R = I = I ₁ + I ₂ + I ₃ = V₁/R₁ + V₂/R₂ + V₃/R₃ =>
1/R = 1/R₁ + 1/R₂ + 1/R₃ [R < R_min<1,2,3>]
1/R_T = Σ 1/R (for // connection)

R_T < R_min: as each resistor has I through it => each resistor ↓ I _T => ↓ R_T (more paths for e^- flow)

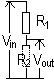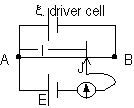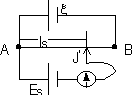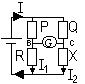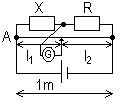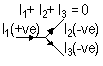
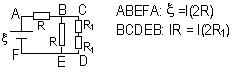
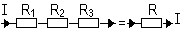
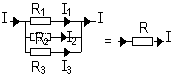
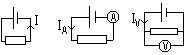
Ammeter	Voltmeter
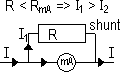
measures current	measure pd bet 2 pts
series connection	// connection w/ device whose potential drop is being measure
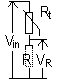
v. low R (should not affect current being measured)	v. high R (negligible I through voltmeter > no pd across voltmeter)
IA = V/(R+RA) RA<<R (RA → 0) => IA → V/R => IA ≈ I	IV = V/RT = V(R+RV)/RRV = V (1/R + 1/RV) RV>>R (RV → ∞) => IV → V/R => IV ≈ I

milliammeter > ammeter: use shunt w/ low R, // connection w/ milliammeter
-shunt has lower R than milliammeter > I flows through shunt

milliammeter > voltmeter: use multiplier w/ high R, series connection w/ milliammeter
-multiplier has higher R > most pd across multiplier


Potential divider
used to take a fraction of input pd for use in another circuit

I = V_in/(R₁+R₂)
V_out = IR₂ = R₂/(R₁+R₂) x V_in
thermistor: -ve temp coefficient: T↓, R↓

V_R = R/(R+R_t) x V_in
T high: R_t ↓, V_r↓, T low: R_t ↓, V_r ↓
LDR can be also used; light intensity ↓: R_LDR ↓, V_r↓
Potentiometer
principle illustrated by 2 identical cells place back-to-back, emf_T =0 V, galvanometer reads 0 A


resistance wire AB connected to stable power supply(driver cell)
l too short: V_E > V_AJ, I ← (E → A), galvanometer deflects left
l too long: V_E < V_AJ, I → (A → E), galvanometer deflects right
at balance: V_E = V_AJ, I = 0 A, galvanometer: 0A, no deflection
at balance, emf E is measured as I = 0A, V = ζ - Ir => V = ζ
before measuring emf; calibrate w/ weston standard cell at 18°C: emf, E_S = 1.0186 V

E/E_S = l/l_S [=V_AJ/V_AJ']
if no balance pt: -wrong connection (not back-to-back), -ζ < E

Wheatsone bridge-to measure resistance

X: unknown resistance
R: resistance adjusted until galvanometer reads 0A (ie balance pt) => potential at (B = C) => V_P = V_Q => V_R = V_X => V_P/V_R = V_Q/V_X
since galvanometer reads 0A: I_P = I_R = I₁ & I_Q = I_X = I₂
V_P/V_R = I₁P/I₁R = P/R
V_Q/V_X = I₂Q/I₂X = Q/X
=> P/R = Q/X

Slide-wire(metre) bridge

since wire is uniform
R_AJ/R_BJ = l₁/l₂ [R=ρl/A, ρ & A: const => cancelled out]
at balance: galvanometer reads 0A
X/R = l₁/l₂

before experiment: check jockey at A & B, should deflect in opp dirⁿs
precaution: do not scrape jockey along wire/ press too hard w/ jockey (spoils wire's uniformity => equation not valid)


Back to 'A' level notes index

Back to notes index