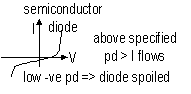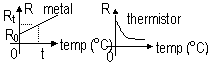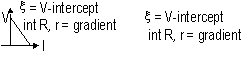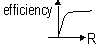CURRENT OF ELECTRICITY
Electric charge
charge(+/-), Q which flows past a pt. in time, t if current, I is constant is defined by Q = It (Q = coulomb, C, 1C = 1As)
if I not const, Q = ∫I dt (area under I-t graph) [Q = It => I = dQ/dt => Q = ∫I dt]
I = nAve [n = # of conduction electrons per unit volume, A = cross-sectional area of wire, v = drift speed/velocity of e^-s, e = electric charge] (I = nAvQ; Q for both + & - charges) (v depends on ion vibration; vib. ^: v decreases (more collisions)
dirⁿ of conventional current = dirⁿ of +ve charges (+ > -)
current, I = rate of flow of charge

Potential difference
-pd bet 2 pts = E converted from elec E to other forms of E when unit charge passes from 1 pt to another
pd = E converted/charge => V= E/Q (1 V = 1 J/C)
-potential at a pt in circuit: usually pd bet pt & arbitrary zero (arbitrary zero: electric earth)
V = E/Q = E/t ÷ Q/t = P/I => pd = power/current (1 V = 1 W/A)

Resistance
-electric property of material that makes moving charges -dissipate energy
-ratio of pd to current, R= pd/current = V/I (R: Ω, ohm, 1 = 1 V/A)

Ohm's Law: I through a metallic conductor is directly ∝ to the pd across its ends, provided temp remains const

grad of V-I graph = R
grad of I-V graph = 1/R



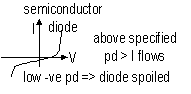
1/R = conductance (S, siemens, 1 S = Ω^-1)

R ∝ l/A => R = k l/A = ρl/A (ρ = resistivity = RA/ l; Ωm)
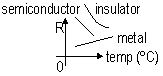
π(Ωm); conductor: ~10⁷, semiconductor: ~10², insulator: ~10¹⁰
R_t = R₀(1 + αt) [α = temp coefficient of resistance]
α = (R_t - R₀) / R₀t


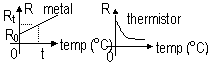
I = nAve: as T ↓
  -metals; n: ~ const (δ), v: ↓ => I: ↓ => R: ↓
  -thermistor; n: ↓, v: ↓ => I: ↓ => R: ↓   -insulator; n: ↓ => I: ↓ => R: ↓
  -semiconductor; n: ↓, v: ↓ => I: ↓ (↓ in charge carriers more significant)=> R: ↓

conductivity = 1/ resistivity = 1/ρ
I = V/R = VA/(ρl) = conductivity x VA/ l ∴ I ∝ conductivity, pd, cross-sectional area & I ∝ 1/wire length

Electromotive force
-E converted from other forms to elec E per unit charge
emf, ζ = energy converted (generated) / charge supplied, ζ = E/Q (ζ: volts, V, 1 V = 1 J/C)
emf of source = pd across source terminal as I → 0

Internal Resistance

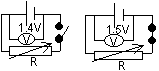
When I flows through resistor: voltmeter shows pd across battery & resistor (voltage drop due to voltage drop in int R)
E transferred per second within battery = E (transferred in circuit & in overcoming int R) per second
Iζ = I²R + I²r
=> ζ = IR +Ir
=> V = IR = ζ - Ir = emf - voltage across int R = terminal pd (pd shown on voltmeter)
good voltmeter: v. high R- accurate reading: terminal pd very close to battery emf

V = IR = ζ -Ir (r: const)
∴ if R (resistance of resistor) is varied and I measured => V-I graph plotted to obtain r


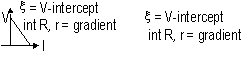
Efficiency
efficiency = power (output / input) = power [to external circuit / used(supplied)] = I²R/Iζ = IR/ζ = IR/(IR+Ir) = R/(R+r)


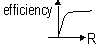
efficiency ≠ 1 unless r = 0
R >> r, efficiency → 1
R = r, efficiency = 50% (max power)


Back to 'A' level notes index

Back to notes index