SUPERPOSITION
when >1 wave w/ same freq overlap => interference (illustrated by ripple tank)

2 sources A & B w/ equal freq giving circular waves
principle of superposition can explain interference pattern
along RS: A_crest and B_crest meet at same time > constructive interference > large wave along RS
along XY: A_crest and B_trough meet at same time > destructive interference > no wave along XY(> every pt on XY: λ/2 nearer to A)
reinforcement: constructive interference- at pt C when path diff AC - BC = kλ (k ∈ Z⁺)
cancellation: destructive interference- at pt C when path diff AC - BC = (k+½)λ (k ∈ Z⁺)

Principle of superposition:
when 2 waves travel through, the resultant displacement at any pt = vector sum of separate displacement due to the 2 waves


Interference of microwaves

max & min detected along AB due to inter. of wave from PQ
Interference of sound waves

2 loudspeakers in // w/ audio freq oscillator microphone/ ear moved along MN: alternate loud & soft

Conditions for 2-source interference
-coherent sources: same freq (=> same λ), in phase/ w/ const phase diff
-~ same amplitude (or else no min)
-for transverse waves: -unpolarised / -polarised in same plane
-for light: sources v.clost as λ of light is v.small (not close: light & dark bands v.close => can't be seen)

Young's double slit experiment

A, B, C: narrow slits, A & B: v. close together
bright & dark bands seen on both sides of O (perpendicular bisector of AB)
[width of slits = 0.2mm, separation of double slit = 0.5mm]
white light used: diff colours > diff λ

P = m^th bright line, BP - AP = mλ
PA = PN = > BN = BP - AP = mλ
AB is v.small > PM >> AB => AN & PN meet at ~90° => ∠PMO ≈ ∠BAN = θ
ΔBAN: sinθ = BN/AB = mλ/a
ΔPMO: tanθ = PO/MO = x_m/D
θ is v.small, tanθ ≈ sinθ => x_m/D = mλ/a => x_m = mDλ/a
Q: neighborring bright fringe- OQ = x_m-1 = (m-1)Dλ/a
∴fringe separation, x = Dλ/a [D: separation of double slit & screen, a: separation of double slit, λ: wavelength of wave]

λ_light: 10^-6m
source slit closer to double slit: x unaffected (only brighter)
source slit widened & widened > fringes gradually disappear (large slit acts as several narrow slits > many interference patterns at diff places > dark & bright fringes overlap > uniform illumination)
white light used: central fringe = white, other fringes = colour
blue fringe (smallest λ) closest to central, red fringe (largest λ) furthest from central


Diffraction = spreading of wave when wave pass through aperture / around obstacles



generally: smaller aperture (compared to λ) > more diffraction
λ_light= 6 × 10^-7m => small objects/ aperture: sig diffraction of light

sound waves can diffract around wide openings as opening comparable to _sound
diff ∝ λ (low notes heard easier than high notes)

Single slit diffraction



A & B: on plane wavefront & can be considered as 2 secondary sources of light, since from same wavefront => coherent w/ identical amplitude =>interference pattern as long as slit is narrow (rel to λ)
short dist beyond M & N (projections of A & B): alternate bright & dark fringes
central fridge: twice as wide as & intensity v.much greater than other bright fringes
sin θ = λ/d (d: separation of double slit)



Increasing # of slits





each slit: similar diffraction effect in same direction > pattern similar to 1 slit w/ intensity variation (but crossed by intermediate fringes due to interference bet slits)
more // equidistant slits; intensity & sharpness of: -principal max increases, -subsidary max decreases
100's slits/mm: only a few sharp principal maxima

diffraction grating: glass/ metal w/ large # of close // equidistant slits ruled on it

grating w/ n lines/mm: d = 1/(n × 10⁴)m
BC = dsinθ = path diff bet 2 adjacent slits
for bright fringe: BC = kλ (k = whole #/0)
=> sinθ = BC/AB = k /d => dsinθ = kλ
1st order bright fringe = 1st adjacent fringe to central fringe


more slits > less # of bright fringes which are brighter

Measurement of wavelength

find 1st order of diffraction on each side => angular diff = 2θ=> λ = dsinθ (k = 1)

Stationary /standing waves
-formed when 2 identical waves (same freq + amp) travel in opp directions in a medium
-wave-like profile doesn't move along medium

N-nodes = pts of permanent zero displacement
A-anti-nodes = pts ½ way bet 2 nodes w/ max amplitude of vibration (vib: 0 ≤ A ≤ 2 amp._original)
dist bet 2 nodes, NN = λ/2, AA = λ/2, AN =λ/4

Modes of vibrations of stretched string

fundamental freq, f₀ (1^st harmonic): l =λ/2 => f₀ = v/λ = v/2l

1^st overtone, f₁ (2^nd harmonic): l =λ₁ => f₀ = v/λ₁ = v/l = 2f₀

2^nd overtone, f₂ (3^rd harmonic): l =3λ₁/2 => f₀ = v/λ₂ = 3v/2l = 3f₀

nth overtone: (n+1)f₀

Stationary waves in air columns
closed pipe- open end always anti-node, closed end = node
open pipe- both ends always anti-node

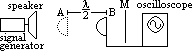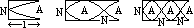
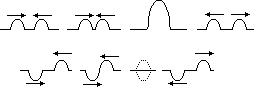
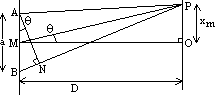
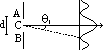
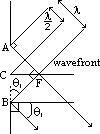
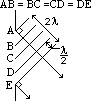
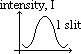
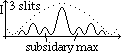
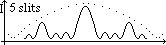
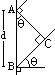
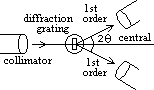
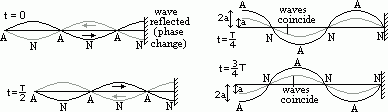
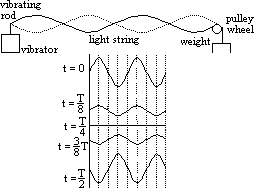
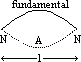
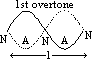
	closed	open
fundamental freq, f0 (1st harmonic)	l =λ/4 => f0 = v/λ = v/4l	l =λ/2 => f0 = v/λ = v/2l
1st overtone, f1 (2nd harmonic)	l =3λ1/4 => f1 = v/λ1 = 3v/4l = 3f0	l =λ1 => f1 = v/λ1 = v/l = 2f0
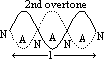
2nd overtone, f2 (3rd harmonic)	l =5λ2/4 => f2 = v/λ2 = 5v/4l = 5f0	l =3λ2/2 => f2 = v/λ2 = 3v/2l = 3f0
nth overtone	(2n+1)f0	(n+1)f0

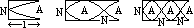
Measuring λ of sound using stationary waves

sound waves of const freq emitted from loudspeaker aimed at reflecting surface > sound reflected > interfere w/ incident waves > stationary waves set up
microphone, connected to y-plates of oscilloscope, moved through region of standing waves
mic placed at 2 successive max pts (anti-nodes- loudest sound) => dist, x, bet pts = λ/2 => λ = 2x
anti-node >(move)> node: loud > soft sound, node >(move)> anti -node: soft > loud sound

Calculate velocity of sound in air by Kurdt's tube


freq of sound varied, resonance occurs when f equals natural freq of vib of air column in tube > stationary waves formed > lycopdium powder collects in heaps at nodes (no disturbance)
av. dist bet 2 heaps/nodes = λ/2

Resonance tube experiments

A: anti-node actually slightly above rim, dist 'c' above rim
at 1^st resonance: l₁ + c = λ/4
at 2^nd resonance: l₂ + c = 3λ/4
l₂ - l₁ = λ/2


Back to 'A' level notes index

Back to notes index